[PJWSTK] ASD – jesień 2015 – Zadanie 4 – Porady

Sam algorytm jest banalny do napisania, ale nie mam zgody twórcy na publikację kodu (rok temu dostał 100%).

Najpierw wytłumaczę o co chodzi w poleceniu:
„Wyznacz liczbę klas abstrakcji zbioru R ustalonych względem relacji binarnej r takiej, że m(i) r m(j) wtedy i tylko wtedy, gdy suma elementów podmacierzy m(i) jest równa sumie elementów podmacierzy m(j), dla 0<=i,j<k. Dodatkowo ustal liczbę klas abstrakcji o maksymalnym rozmiarze oraz średnią wartość sum elementów podmacierzy stanowiących zbiór R zredukowaną do jej części całkowitoliczbowej.”

Tłumacząc to na 'nasze’:
1. mamy macierz kwadratową X (którą trzymamy jako tablice 2 wymiarową)
2. potem dostajemy dużo linijek, a w każdej 4 liczby które wyznaczają 'lewy górny’ i 'prawy dolny’ róg 'podmacierzy’ (czyli prostokąta)
3. dla każdej podmacierzy musimy wyliczyć sumę elementów

Na wyjściu musimy wyświetlić 3 liczby:
(liczba klas abstrakcji, liczba klas abstrakcji o maksymalnym rozmiarze, średnia wartość sum elementów podmacierzy należących do zbioru R)

Najpierw 2 definicje:
klasa abstrakcji – suma elementow podmacierzy
rozmiar klasy abstrakcji – ilosc podmacierzy o konkretnej sumie elementow podmiacierzy

Teraz co wyświetlić:
1. ilość podmacierzy o różnych sumach elementów (czyli jak dwie lub więcej podmacierzy ma taka samą sumę elementów to do tego licznika dodajemy ją jako jedną podmacierz)

2. (najdziwniejszy punkt):
mozemy miec klasy abstakcji ktore zapiszemy w 'map’ w C++ (przykład: mielismy 14 podmacierzy, ale suma ich elementow dawala tylko 4 rozne wyniki):
suma elementow podmacierzy -> ilosc wystapien
390 – 3
293 – 5
43 – 5
178 – 1
a na wyjsciu ma byc: 2, bo maksimum to 5, a ilosc wystapien maksimum to wlasnie 2

3. banał, sumować wszystkie 'sumy podmacierzy’ i podzielić przez ich ilość (czyli 'k’), operowac na int (long long int) to sie samo zaokragli w dół zgodnie z poleceniem
Teraz cały problem z algorytmem:
Obliczanie sum podmacierzy to masa dodawania która zajmie 'za dużo czasu’. Zamiast tego można uzyskać sumę elementów jedną linijką obliczeń:

sumaElementowPodmacierzy = 
  macierz[wierszDolny+1][kolumnaPrawa+1] + 
  macierz[wierszGorny][kolumnaLewa] - 
  macierz[wierszGorny][kolumnaPrawa+1] - 
  macierz[wierszDolny+1][kolumnaLewa];

Tylko najpierw przy wczytaniu macierzy trzeba zapisac w kazdej komorce macierzy 'sume elementow w gore i lewo od tej komorki z jej wartoscia włącznie’ zamiast 'jej wartosci’ – co mozna tez obliczac jedna linijka.
Dla ulatwienia obliczen mozna utworzyc macierz kwadratową o rozmiarze 'n+1′ zamiast 'n’ i w pierwsza linijke/pierwsza kolumne wpisac same zera.

Rysunek pomocniczy:

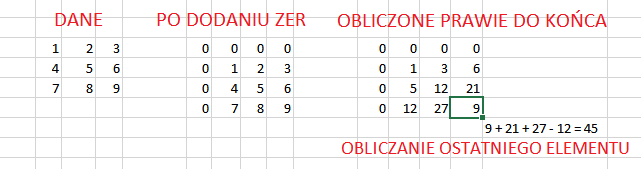
Ważne, żeby pamiętać o używaniu w większości miejsc 'long long int’.

Gotowy program ma mniej, niż 100 linijek i składa się z paru pętli 'for’ oraz jednej 'pętli po mapie’. Rozwiązanie rok temu dostało 100%, ale nie mogę go publikować.

— DLA GOOGLE —

ZADANIE NUMER 4

Rozważmy macierz kwadratową M rozmiaru n, której elementy są liczbami całkowitymi. Dalej R={m(0),m(1),…,m(k-1)}jest zbiorem k różnych podmacierzy macierzy M (przez podmacierz rozumiemy spójny fragment macierzy właściwej o zadanych indeksach elementów krańcowych).
Wyznacz liczbę klas abstrakcji zbioru R ustalonych względem relacji binarnej r takiej, że m(i) r m(j) wtedy i tylko wtedy, gdy suma elementów podmacierzy m(i) jest równa sumie elementów podmacierzy m(j), dla 0<=i,j<k. Dodatkowo ustal liczbę klas abstrakcji o maksymalnym rozmiarze oraz średnią wartość sum elementów podmacierzy stanowiących zbiórR zredukowaną do jej części całkowitoliczbowej.

WEJŚCIE

Wiersz zawierający liczby n oraz k oddzielone znakiem odstępu (kod ASCII 32) i zakończony znakiem nowej linii (kod ASCII 10). Następnie n wierszy reprezentujących kolejne wiersze macierzy M, w których elementy rozdzielone są znakiem odstępu, a każdy wiersz zakończony jest znakiem nowej linii. Dalej k wierszy, z których każdy reprezentuje podmacierz m(i), dla i=0,1,…,k-1, postaci:
– liczba określająca indeks wiersza lewego górnego „rogu” podmacierzy m(i), znak odstępu,
– liczba określająca indeks kolumny lewego górnego „rogu” podmacierzy m(i), znak odstępu,
– liczba określająca indeks wiersza prawego dolnego „rogu” podmacierzy m(i), znak odstępu,
– liczba określająca indeks kolumny prawego dolnego „rogu” podmacierzy m(i), znak nowej linii.
Zakładamy indeksowanie wierszowe i kolumnowe elementów macierzy M od 0 do n-1 włącznie.

WYJŚCIE

Wiersz zawierający trzy liczby całkowite oddzielone znakiem odstępu (liczba klas abstrakcji, liczba klas abstrakcji o maksymalnym rozmiarze, średnia wartość sum elementów podmacierzy należących do zbioru R) stanowiące rozwiązanie problemu.

OGRANICZENIA

Liczby n i k ograniczone kolejno od dołu przez 1, od góry odpowiednio przez 10^4 oraz 10^8. Elementy macierzy Mograniczone przedziałem [-10^3,10^3].

LIMITY

Oczekiwana złożoność czasowa rzędu O(n^2+klgk). Oczekiwana złożoność pamięciowa rzędu O(n^2+k).

PRZYKŁAD 1

wejście:
4 8
-2 -2 -3 1
3 0 1 3
1 3 -3 3
2 0 0 -2
0 0 2 1
2 2 2 3
1 2 1 3
3 2 3 3
3 0 3 3
0 1 2 1
3 3 3 3
1 3 1 3

wyjście:
5 3 0

/* KOMENTARZ DO ROZWIĄZANIA
Oznaczmy przez SM0, SM1, …, SM7 sumy elementów kolejnych podmacierzy podanych na wejściu, wtedy:
SM0=(-2)+(-2)+3+0+1+3=3
SM1=(-3)+3=0
SM2=1+3=4
SM3=0+(-2)=(-2)
SM4=2+0+0+(-2)=0
SM5=(-2)+0+3=1
SM6=(-2)
SM7=3
Stąd liczba klas abstrakcji względem rozważanej relacji jest równa 5 (różne wartości w/w sum to kolejno (-2), 1, 0, 3 oraz 4). Dalej, liczba klas abstrakcji o maksymalnym rozmiarze równa jest 3, są to klasy abstrakcji elementów (-2), 0 oraz 3. Ostatecznie średnia wartość sumy elementów rozważanych podmacierzy zredukowana do części całkowitoliczbowej to:
(3+0+4+(-2)+0+1+(-2)+3)/8=7/8=0
Zatem odpowiedź stanowi trójka liczb 5, 3 oraz 0. */

PRZYKŁAD 2

wejście:
8 8
-5 -4 -6 -2 1 -8 6 -1
-9 7 -3 -7 2 0 -6 -2
6 -8 2 6 -7 0 3 -5
-1 3 9 4 -7 0 -5 -3
-8 0 0 -6 -5 -7 -7 0
2 7 6 2 -6 6 5 0
-1 -7 8 -7 6 7 -2 1
-8 -3 -5 2 -5 4 -1 -2
0 2 3 6
2 6 4 6
0 7 1 7
7 4 7 4
1 7 7 7
2 7 6 7
4 5 6 5
6 2 7 5

wyjście:
8 8 -4

PRZYKŁAD 3

wejście:
16 24
1 -9 7 1 8 -5 0 -7 -2 5 7 -1 -5 -1 0 8
-6 2 0 5 -5 -3 0 3 6 9 2 9 7 9 7 1
4 -6 -1 -6 2 -4 -7 -3 1 0 8 8 2 6 1 6
5 0 0 6 -5 -5 -8 -9 -3 -5 2 -1 -1 9 4 -8
9 -5 -6 -2 0 -5 7 1 7 0 -9 -3 -9 -6 0 -9
6 9 2 5 -6 -2 -6 0 0 4 3 -5 7 -4 -4 9
-4 -8 6 -6 3 5 -3 -8 5 -5 9 -8 -2 3 7 6
2 -1 -1 8 7 -5 -8 1 1 0 7 0 4 6 9 -4
-9 -9 0 4 -2 8 -1 6 8 5 -3 -9 1 -7 0 8
-8 7 8 8 -1 3 0 -6 -4 -2 1 -9 2 -5 -4 -8
-3 -1 9 8 8 1 -6 8 -4 -8 0 -7 -7 -9 -4 6
0 -2 7 -1 6 7 1 2 9 -7 -6 8 -2 7 -2 9
-9 1 -8 -3 7 4 4 -1 9 -8 8 5 8 9 8 -2
-8 -5 5 -8 5 8 4 -4 1 5 9 -5 -8 5 -6 -8
1 6 0 -7 9 9 7 -1 0 0 4 5 9 5 -8 -1
-5 -5 2 6 7 9 6 -6 -8 -9 -3 9 -9 -8 9 5
2 11 15 15
12 12 12 12
15 7 15 15
10 1 13 14
0 14 8 15
8 13 9 13
11 2 12 7
0 2 15 15
12 13 15 13
1 10 14 11
13 7 13 15
14 14 14 14
15 6 15 6
8 9 8 15
11 5 15 9
15 6 15 10
10 12 14 15
7 12 14 13
14 4 14 13
9 13 15 15
4 4 7 12
12 6 14 12
11 7 11 15
10 2 11 4

wyjście:
21 3 20